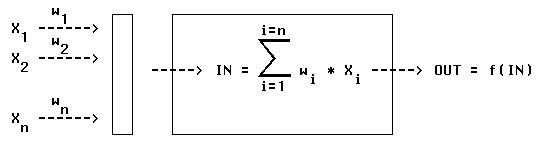
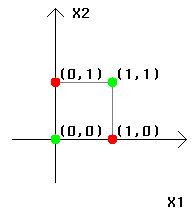
Figure 3-1
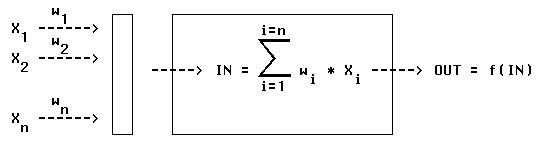
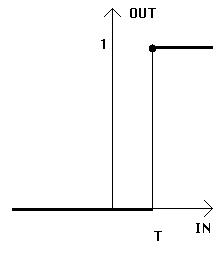

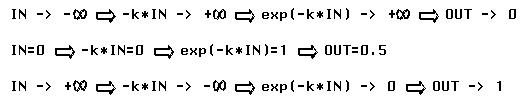
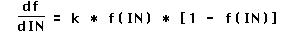
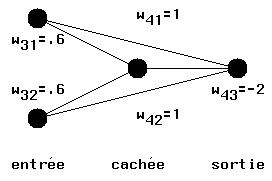
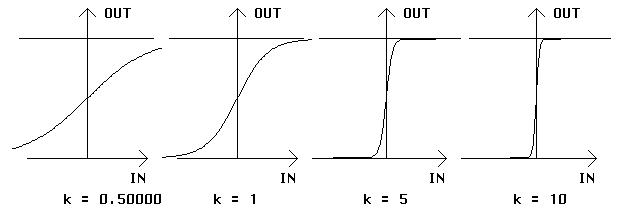 Figure 3-3
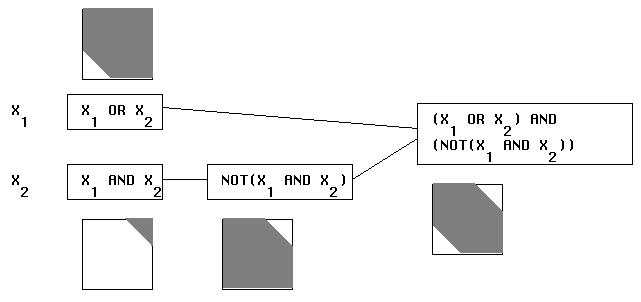
Figure 3-3
| X1 | X2 | w1 * X1 + w2 * X2 | IN |
| 0 | 0 | 0 < T | 0 |
| 1 | 0 | w1 < T | 0 |
| 0 | 1 | w2 < T | 0 |
| 1 | 1 | w1 + w2 > T | 1 |
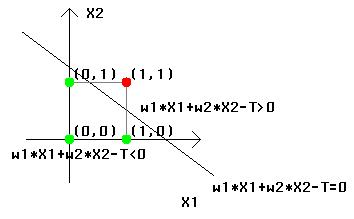
| X1 | X2 | w1 * X1 + w2 * X2 | IN |
| 0 | 0 | 0 < T | 0 |
| 1 | 0 | w1 > T | 1 |
| 0 | 1 | w2 > T | 1 |
| 1 | 1 | w1 + w2 > T | 1 |
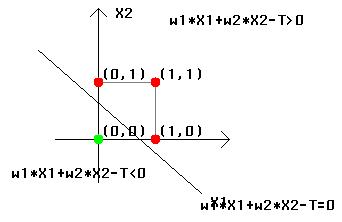
| X | w * X | IN |
| 0 | 0 = T | 1 |
| 1 | w < T | 0 |
| X1 | X2 | XOR(X1, X2) |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
| X1 | X2 | e3 = w13 * a1 + w23 * a2 | a3 | e4 = w14 * a1 + w24 * a2 + w34 * a3 | a4 |
| 0 | 0 | 0 * .6 + 0 * .6 = 0 | 0 | 0 * 1 + 0 * 1 + 0 * (-2) = 0 | 0 |
| 0 | 1 | 0 * .6 + 1 * .6 = .6 | 0 | 0 * 1 + 1 * 1 + 0 * (-2) = 1 | 1 |
| 1 | 0 | 1 * .6 + 0 * .6 = .6 | 0 | 1 * 1 + 0 * 1 + 0 * (-2) = 1 | 1 |
| 1 | 1 | 1 * .6 + 1 * .6 = 1.2 | 1 | 1 * 1 + 1 * 1 + 1 * (-2) = 0 | 0 |
| X1 | X2 | X1 OR X2 | X1 AND X2 | NOT(X1 AND X2) | (X1 OR X2) AND (NOT(X1 AND X2)) = XOR |
| 0 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 |
| X1 | X2 | OUT (calculee) | OUT0 (souhaitee) | corrections (dw) |
| 0 | 0 | 0 = | 0 | |
| 1 | 0 | 1 > | 0 | w1 -= dw |
| 0 | 1 | 1 = | 1 | |
| 1 | 1 | 0 < | 1 | w1 += dw w2 += dw |
| w1 | w2 | w0 | X1 | X2 | w1*X1+w2*X2+w0*X0 | OUT | OUT0 | correction |
| 0.5 | 0.6 | -0.3 | 0 | 0 | 0 + 0 - 0.3 = -0.3 | 0 | 0 | . |
| 0.5 | 0.6 | -0.3 | 1 | 0 | 0.5 + 0 - 0.3 = 0.2 | 1 | 0 | w1-=dw w0-=dw |
| 0.4 | 0.6 | -0.4 | 0 | 1 | 0 + 0.6 - 0.4 = 0.2 | 1 | 0 | w2-=dw w0-=dw |
| 0.4 | 0.5 | -0.5 | 1 | 1 | 0.4 + 0.5 - 0.5 = 0.4 | 1 | 1 | . |
| w1 | w2 | w0 | X1 | X2 | w1*X1+w2*X2+w0*X0 | OUT | OUT0 | correction |
| 0.4 | 0.5 | -0.5 | 0 | 0 | 0 + 0 - 0.5 = -0.5 | 0 | 0 | . |
| 0.4 | 0.5 | -0.5 | 1 | 0 | 0.4 + 0 - 0.5 = -0.1 | 0 | 0 | . |
| 0.4 | 0.5 | -0.5 | 0 | 1 | 0 + 0.5 - 0.5 = 0 | 1 | 0 | w2-=dw w0-=dw |
| 0.4 | 0.4 | -0.6 | 1 | 1 | 0.4 + 0.4 - 0.6 = 0.2 | 1 | 1 | . |
| w1 | w2 | w0 | X1 | X2 | w1*X1+w2*X2+w0*X0 | OUT | OUT0 | correction |
| 0.4 | 0.4 | -0.6 | 0 | 0 | 0 + 0 - 0.6 = -0.6 | 0 | 0 | . |
| 0.4 | 0.4 | -0.6 | 1 | 0 | 0.4 + 0 - 0.6 = -0.2 | 0 | 0 | . |
| 0.4 | 0.4 | -0.6 | 0 | 1 | 0 + 0.4 - 0.6 = -0.2 | 0 | 0 | . |
| 0.4 | 0.4 | -0.6 | 1 | 1 | 0.4 + 0.4 - 0.6 = 0.2 | 1 | 1 | . |