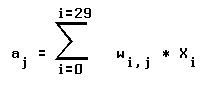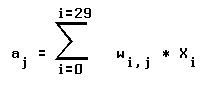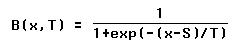LES RÉSEAUX NEURONAUX: PERCEPTRON

Définition
Apprentissage
Exemple
Perceptron probabiliste

Définition

         On a vu précédemment le fonctionnement d´un neurone artificiel. Un réseau neuronal s´obtient en branchant des sorties de certains neurones sur les entrées d´autres neurones.
         Le perceptron est le premier réseau neuronal conçu par Rosenblatt (1958), il vise à associer des réponses à des patterns présentés en entrée (problèmes de reconnaissance). Il se compose de deux couches de neurones:
         1) La première couche, ou rétine est composée de cellules binaires perceptives (OUT = 0 ou 1).
         2) La deuxième couche fournit la réponse.
         Par exemple la rétine peut comporter 5 * 6 cellules et la sortie 10 cellules. Le problème est de reconnaître un chiffre (parmi 0,1,2,3,4,5,6,7,8,9) impressionant la rétine. Si le chiffre 4 est présentée, la cinquième cellule de sortie doit être active et toutes les autres doivent être passives.
         Toutes les cellules de la rétine sont reliées à chacune des cellules de la sortie par des poids variables. Si les cellules de la rétine sont indexées par i (variant de 0 a 29) et celles de la sortie sont indexées par j (variant de 0 a 9), l´entrée a_j d´une cellule de sortie j est la somme pondérée de toutes les sorties des cellules de la rétine (voir figure 4-1):

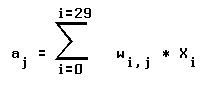
             a_j = entrée de la cellule j de sortie.
             x_i = sortie (0 ou 1) de la cellule i de la rétine.
             w_i,j = poids de la liaison i-> j.
         Une fonction seuil permet alors de déterminer la sortie de la cellule j:
             x_j = (a_j <= T) ? 0 : 1
         On peut remplacer le seuil T par un seuil nul a condition d´ajouter une cellule de la rétine toujours active et de poids -T.

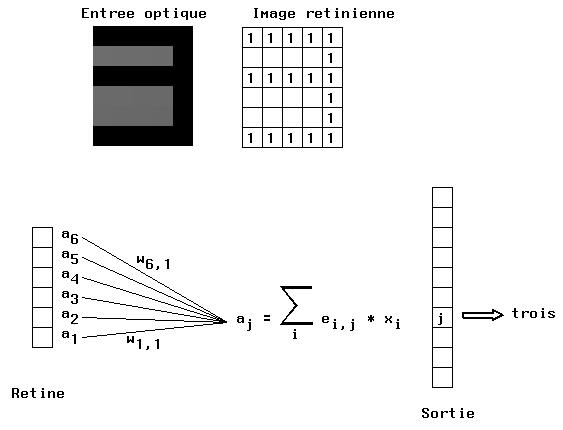
Figure 4-1

Apprentissage

       Règle d´apprentissage
       Théorème de convergence du perceptron
       Ajustement de la constante d´apprentissage

Règle d´apprentissage

         La règle la plus connue est celle dite de Widrow-Hoff (1960) ou règle du delta. Ell est locale, c´est à dire que chaque cellule de sortie apprend indépendamment des autres.
         Une cellule de sortie ne modifie les poids des liaisons qui aboutissent à elle que si elle se trompe:
         Si elle est active alors qu´elle devrait être passive alors elle diminue les poids correspondant aux cellules actives de la rétine.
         Si elle est passive alors qu´elle devrait être active alors elle augmente les poids correspondant aux cellules actives de la rétine.
         L´algorithme de l´apprentissage se déroule de la façon suivante:
         1) On présente au perceptron (dans un ordre arbitraire) les couples (image sur la rétine, réponse).
         2) S´il y a des erreurs alors les poids sont corrigés selon la règle du delta et on retourne en 1, sinon le perceptron a appris.
         La règle de Widrow-Hoff peut s´écrire:
         w_i,j(t + 1) = w_i,j(t) + n * (t_j - o_j) * x_i = w_i,j(t) + dw_i,j
             w_i,j(t + 1) = poids de la liaison i -> j au temps t + 1
             w_i,j(t) = poids de la liaison i -> j au temps t
             x_i = sortie (0 ou 1) de la cellule i de la rétine
             o_j = réponse de la cellule j de sortie
             t_j = réponse théorique (souhaitée) de la cellule j de sortie
             n = constante positive (entre 0.0 et 1.0): Une bonne valeur est 0.75, mais il est préférable de faire évoluer n au cours du temps: D´abord grande (0.9) puis décroissante au cours de l´apprentissage.

Théorème de convergence du perceptron

         On démontre que si une solution au problème existe alors le perceptron, la trouvera en un nombre fini de cycles d´apprentissages.
         Mais on montre que, comme pour un neurone artificiel, le perceptron ne peut résoudre que des problèmes linéairement séparables.
         Pour traiter des problèmes non linéairement séparable on complexifie le perceptron en lui ajoutant une couche (dite couche cachée) de neurones, en faisant un réseau neuronal plus général. C´est ce que fit Rosenblatt en 1962 pour résoudre le probleme du XOR. Mais la correction des poids devient problématique puisqu´elle modifie les entrées de la couche cachée et donc ses sorties...
         La technique, dite de rétro-propagation de l´erreur fut trouvée en 1969 par Bryson et Ho, puis redécouverte en 1986 en particulier par Rumelhart.

Ajustement de la constante d´apprentissage

         perceptron P v
         Prend par défaut n = 0.1 constant
         perceptron P v e=0.9 c=0.6
         Prend n = 0.9 multiplié par 0.6 à chaque itération (donc n décroît au cours de l´apprentissage).
         La figure 4-2 montre les variations du nombre d´erreurs au cours de l´apprentissage dans ces deux cas. On remarque que lorsque n est d´abord grand puis diminue le perceptron converge plus rapidement: En effet de grandes corrections au début permettent de discriminer rapidement des patterns très différents, puis de petites corrections à la fin permettent des ajustements ne détruisant pas les reconnaisances dejà acquises.

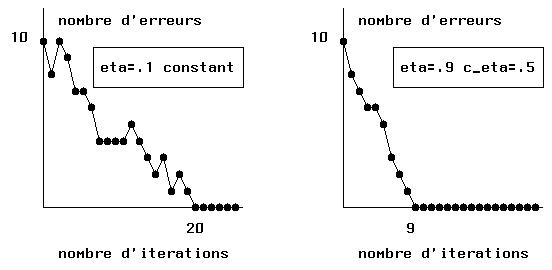
Figure 4-2 A titre d´exercice, faire tourner le programme perceptron en faisant varier les constantes eta et c_eta.

Exemple

Le programme perceptron

         Voici la déscription d´un perceptron élémentaire reconnaissant des patterns parmi un vocabulaire donné (voir le source perceptron.c):
         Lancement: perceptron P v
         perceptron est le nom du programme
         P est un fichier contenant la déscription de Np patterns sous la forme de matrices Nx * Ny contenant des 0 et des 1.
         v indique une exécution en verbose.
         Il y a 1000 passes d´apprentissage au maximum par defaut, pour augmenter ce nombre:
         perceptron P v n=2000
         Par exemple, pour les chiffres, le fichier P est de la forme:
   11111   00100   11111   11111   01000   11111   11111   11110   11111   11111
   10001   00100   00001   00001   01000   10000   10000   00010   10001   10001
   10001   00100   11111   11111   01010   10000   10000   00010   11111   11111
   10001   00100   10000   00001   01010   11111   11111   00111   10001   00001
   10001   00100   10000   00001   01111   00001   10001   00010   10001   00001
   11111   00100   11111   11111   00010   11111   11111   00010   11111   11111
         Définit Np = 10 patterns avec Nx = 5 et Ny = 6
         lire_fic(argv[1]); Lit ce fichier dans Np tableaux de Nx * Ny éléments dont les adresses sont stockées dans Patterns.
         init_poids(); Initialise aléatoirement les poids dans Np tableaux de Nx * Ny float dont les adresses sont stockées dans Poids. Le tableau numéro num est la liste des poids joignant la rétine à la sortie de même numéro.
         verifier(); Imprime les données.
         apprentissage(eta, c_eta); est la boucle d´apprentissage qui présente successivement sur la rétine les patterns dans un ordre aléatoire: chainer() chaine circulairement les Np patterns, suivant(num, np) retourne un suivant aleatoire parmi np et le retire de la liste.
         evaluer_perceptron(num) calcule les Np sorties pour le pattern num.
         Il y a des erreurs dans 2 cas:
         1) Une cellule est activée alors qu´elle ne devrait pas l´être (par exemple si le pattern 3 est présenté et que la cellule 4 réagit).
         2) Une cellule n´est pas activée alors qu´elle devrait l´être (par exemple si le pattern 3 est présenté et que la cellule 3 ne réagit pas).
         Dans ce cas il faut corriger les poids: On diminue les poids joignant les cellules actives de la rétine à la sortie dans le premier cas, et on augmente ces poids dans le deuxième cas. La formule de Widrow-Hoff
         w_i,j(t+1) = w_i,j(t+1) + n * (t_j - oj) * x_i
devient dans le premier cas:
         w_i,j(t+1) = w_i,j(t+1) + n * (0 - 1) * 1 = w_i,j(t+1) - n
et dans le deuxieme cas:
         w_i,j(t+1) = w_i,j(t+1) + n * (1 - 0) * 1 = w_i,j(t+1) + n
         S´il n´y a plus d´erreur, un break fait sortir de la boucle d´apprentissage.
         Le programme demande alors des noms de fichiers (contenant des patterns de mêmes dimensions que ceux ayant servi à l´apprentissage).
         Si ce pattern appartient à ceux-la, il est reconnu.
         Sinon, soit il n´est pas non reconnu, soit un ou plusieurs patterns proches sont proposés.
         A titre d´exercice, ecrire un fichier codant les lettres de l´alphabet (par exemple les majuscules A B ... Z), ecrire plusieurs fichiers contenant quelques unes de ces lettres, certaines étant bruitées.
         Est-il possible de trouver un alphabet que le perceptron ne reconnait pas ?

Perceptron probabiliste

Distribution de Boltzmann
Variation de la température

Distribution de Boltzmann

         Le perceptron decrit ci-dessus est déterministe, c´est à dire que le même apprentissage donnera chaque fois la même matrice des poids. Si on décide de remplacer la condition:
         x_j = (a_j <= T) ? 0 : 1
         par:
         x_j = (a_j <= T) ? 0 : 1 avec la probabilité p augmentant avec x_j
         Plus l´activation du neurone est élevée, plus celui-ci aura tendance à repondre 1.
         Un tel neurone s´approche plus de la réalite biologique, les êtres vivants ayant rarement un comportement strictement déterministe. D´autre part, lors d´un apprentissage, si le perceptron est déterministe il cesse d´apprendre dès qu´il ne se trompe plus, et sa stratégie, parfaitement adaptée à l´échantillon d´apprentissage, ne convient plus pour d´autres échantillons, provenant de la même population statistique, mais non appris (il a placé sa fonction discriminante trop proche des bords de cet échantillon): Le perceptron généralise alors mal son apprentissage.
         Pratiquement on convertit d´abord l´activation a_j d´un neurone (a_j pouvant prendre n´importe quelle valeur rélle) en une probabilité p (entre 0 et 1), puis on convertit p en une valeur d´activation effective.
         Si on utilise la distribution de Boltzmann, la probabilité de trouver une valeur inférieure ou egale à x est :

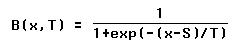
         S est le seuil, et T est la "température"
         Soit p un aléatoire de l´intervalle [0,1], si x est l´activation d´un neurone, sa réponse est:
         o = (x <= p) ? 0 : 1
         Par exemple soit x=0.8 l´entrée du neurone, on a B(x,T)=0.69, si on tire le nombre aléatoire p=0.312, comme x>p la réponse est o=1.
         La figure 4-3 montre une distribution de Boltzmann et sa dérivée. Celle-ci ressemble a la courbe en cloche d´une loi normale et s´exprime par:
         B´(x,T) = B(x,T) * [1 - B(x,T)]

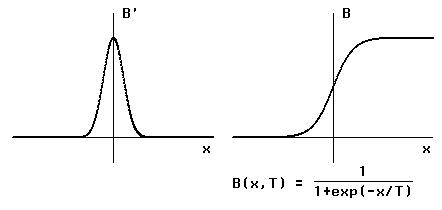
Figure 4-3

Variation de la température

Le paramètre T de température correspond à l´incertitude sur le comportement du système. La figure 4-4 montre les aspects de la distribution de Boltzmann pour différentes températures. Lorsque T tend vers zéro la distribution se rapproche d´une fonction seuil (en escalier), le perceptron redevient déterministe. Pour un T infini la probabilité d´avoir o=1 vaut 0.5 quelque soit l´entrée du neurone dont le comportement devient imprévisible. Pour des températures non nulles ni infinies, plus T est petit plus le perceptron est prévisible et plus T est grand plus il est imprévisible.

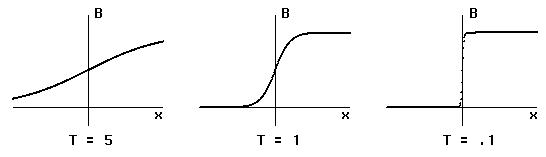
Figure 4-4 Pour T grand le perceptron explore l´espace des valeurs possibles des connexions, mais il ne restera pas dans une région optimale. On commence donc l´apprentissage avec de grandes valeurs de T, puis on diminue T. Cette technique s´appelle le recuit simulé (simulated annealing) qui ressemble à la détrempe d´un métal:
Pour fabriquer une pièce métallique on fait fondre un cristal (arrangement régulier de molécules) dans un moule puis on le rend solide à nouveau en le refroidissant. Augmenter la température revient à augmenter le rayon des déplacements aléatoires des atomes. Refroidir revient à diminuer ce rayon. Mais certains atomes, qui se sont déplacés plus loin que d´autres, peuvent être empéchés de retrouver leur position initiale par d´autres atomes qui, s´étant moins éloignés, la retrouvent plus vite (voir figure 4-5): Il apparait une impureté. La technique du recuit simulé consiste alors à réchaufer très lentement le métal, les rayons de déplacements aléatoires augmentent alors un peu et les atomes s´écartent suffisamment pour que les atomes piégés puissent regagner leur position d´équilibre. On refroidit alors doucement le cristal pour qu´aucun autre atome ne se laisse piéger.

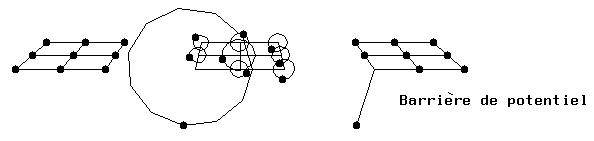
Figure 4-5