PERSPECTIVE
Historique
Définition
On désigne traditionnellement sous le terme de perspective
une technique de projection de l´espace tridimensionnel sur
un plan de telle sorte que la vision de l´image obtenue corresponde
à celle de l´espace.
Mais le mot vient du latin perspicere (ou "voir
clairement") qui a donné perspectiva concernant essentiellement
l´optique. C´est la Renaissance qui a introduit la
distinction entre la perepectiva naturalis (science de
la vision) et la perspectiva artificialis (méthode de projection).
Le Quattrocento italien a inventé la perspective comme
mode de rationalisation de la vision et, donc, de la connaissance.
Il est étonnant de constater que cette découverte a été faite par
des artistes (Brunelleschi 1377-1446 était un sculpteur
et un architecte, et Alberti 1404-1472 était un
architecte lettré) et qu´elle n´a été reprise et théorisée
que beaucoup plus tard, au XVIIe siècle, par des
mathématiciens comme Desargues (1593-1662) qui posèrent
les bases de la géométrie descriptive (Monge 1746-1818) et de la
géométrie projective (Poncelet 1788-1867).
Dans un sens plus large le terme de perspective désigne
toute méthode de figuration plane de l´espace. C´est ainsi que l´on
peut parler d´une certaine forme de perspective à propos
des peintures rupestres puisque l´on y décele des ordonnancement
en profondeur, et même des corrections de parallaxes (comme le firent
les grecs pour les colonnes de leurs temples), bien qu´aucun
système n´en codifie l´usage. On parlera de perspective à
registre du IIIe millénaire au VIe siècle
av JC en Egypte et en Mésopotamie: Les motifs sont alignés
rythmiquement de profil sur des registres superposés dans le plan.
L´antiquité a utilisé la perspective dite en arête de poisson.
On peut également parler d´une perspective rayonnée
caractérisant l´art indien, bouddhique, tibétain et khmer: Spirales
organisant l´image sur le modèle de la pensée indouiste. Les
arts chinois et japonais utilisèrent une perspective aérienne
depuis le Ve siècle, et qui influença la peinture
impressionniste du XIXe siècle européen.
On attribue à Brunelleschi (1377-1446) l´invention de
la perspective avec ses deux petits panneaux peints représentant
les vues du Baptistere de Florence et de la place de la Seigneurie,
sorte de dispositif illusionniste. Ces experiences devaient être
théorisees par Alberti.
Dürer (1471-1528) inventa un appareil de mise en perspective,
en tout point analogue à un appareil photographique dans lequel
les rayons lumineux étaient remplacés par des fils.

Dürer: Théorie de la perspective.
De nombreux peintres (dont Canaletto 1697-1768) utilisèrent
des "chambres noires" qui permettent de relever la projection d´une
scène éclairée.
Botticelli (1444-1510), bien que connaissant parfaitement la
perspective linéaire, se permettait d´inventer des variations. Par exemple
dans "Portrait d´un inconnu", la
perspective des berges de la rivière, en arrière plan, est déviée
de façon à épouser la silouhette du personnage, répondant
à un souci de réalisme (vision binocculaire) et à un parti pris
stylistique.


Botticelli: Portrait d´un inconnu" (Florence, Musee des Offices 1473)
Crise de la perspective
La physique moderne, en nous obligeant à repenser la notion d´espace
(la Théorie de la Relativité, par exemple, en définit la courbure
comme fonction des masses), transforme ses modes de représentation.
L´espace perspectif de la Renaissance
apparait alors comme fortement lié a cette époque.
Alors même que la
géométrie euclidienne
perdait son privilège d´être le seul modèle réel de l´espace,
l´art remettait en cause sa fonction traditionnelle de mimesis
en se concevant comme connaissance et langage: Cézanne (1830-1906)
fait de la peinture un instrument d´analyse, et le Cubisme
brise définitivement la perspective centrale en
représentant simultanément plusieurs "vues" du modèle.

Picasso: Boisgeloup, Musee d´Art Moderne de New York (1932)
La perspective linéaire reste cependant un langage,
avec sa rhétorique (Giorgio
de Chirico), et sa fonction symbolique (Magritte).
D´ailleurs l´Impressionnisme ne l´a pas véritablement remise en cause,
et lorsque Van Gogh semble la tordre, c´est plutôt par la couleur qu´il
veut signifier la profondeur.

Van Gogh: Arles 1888, Amsterdam
Mais la perspective résulte plus d´une construction mathématique
que d´une observation expérimentale,
elle suppose en effet un oeil unique, fixe et ponctuel. La réalite
est bien différente: La vision, d´abord, est binocculaire, ensuite
l´oeil, loin d´être fixe, analyse une scène par une série de saccades
très rapides, échantillonnant avec un cône de très petite ouverture,
enfin l´image rétinienne est courbe. La perception de la profondeur
fait intervenir le temps, la mémoire et un codage culturel de
l´information.
Forme symbolique
Hauck, professeur allemand
de géométrie descriptive, étudia en 1879 ("La perspective
subjective et les courbures horizontales du Style dorique") les
rapports de l´image rétinienne "courbe" et de l´image perspective
"linéaire". Il décela aussi dans certaines fresques pompéinnes un
système perspectif qui, bien que différent de la perspective
linéaire, permettait de représenter les plafonds à caissons et les
sols carrelés (perspective dite en arête de poisson).
Hauck montra ainsi qu´il pouvait exister des systèmes rigoureux
de représentation de l´espace autres que la perspective renaissante
qui n´étaient ni faux ni approchés mais simplement
autres.
Kern ("Précédents de la perspective centrale dans
l´art italien du XVIe siècle") replaça, en 1912,
la découverte de la perspective par Brunelleschi au début du XVe
siècle dans son contexte historique: Dès le IXe siècle les
artistes utilisent une perspective en arêtes de poisson
symétrique qui devient, plus tard, partiellement convergente pour,
à la renaissance, converger au point de fuite:
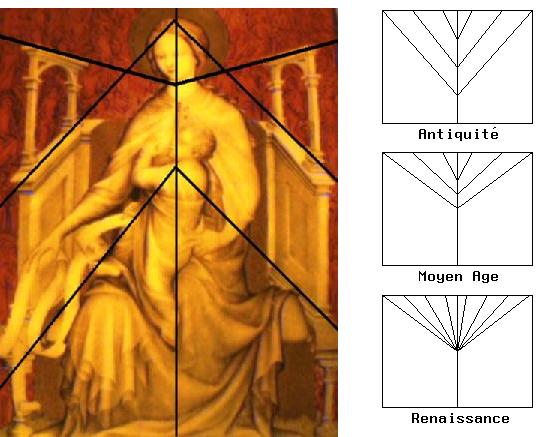
Vierge en majeste, miniature des Tres belles heures
Bibliotheque Royale, Btuxelles
Mesnil, en 1927, montra que la perspective du quattrocento
n´obéissait pas à des exigences de réalisme mais plutot à une volonét
d´abstraction (celle de la projection géométrique) de la renaissance
par opposion à la pensée religieuse du Moyen Age (voir Couchot
"De l´optique au numérique", 1989):
la perspective permettait d´unifier logique et représentation.
Panofsky ("La perspective comme forme symbolique") montra, en 1967,
que chaque époque construit, en le représentant, son propre espace.
Le caractère symbolique de tout espace figuratif devait renouveler
profondément la critique artistique.
Francastel mène une étude sociologique de l´espace figuratif
en examinant parallèlement la perspective de la Renaissance, l´espace
sensible des impressionnistes et l´espace polyvalent de l´art
contemporain: Il définit l´espace figuratif comme tributaire
d´une époque donnée et assemblant une forme à un contenu,
ou encore une géométrie à une mythologie.
White, vers 1950, montra que la perspective linéaire
est un système rigoureux qui a une fonction d´illusion ou
stylistique (comme l´avait déjà dit Mesnil), mais sans
fondement naturel. Parallèlement, il montre qu´il
existe une perspective "courbe", qu´il appelle
perspective synthétique, plus empirique mais plus
proche de la réalite visuelle (tenant compte de la courbure de la rétine,
des points de fuite latéraux et verticaux) et que l´on trouve
déjà dès l´antiquité, qui a été utlisée par des peintres comme
Fouquet (1420-1480) et qui a été théorise par
Léonard de Vinci
(1452-1519).
La synthèse
La synthèse d´image reprend telle quelle la perspective de la
Renaissance, n´en retenant que l´algorithme simpliste de la
projection conique, oubliant toutes les variations inventées
par les artistes depuis le quattrocento pour lui faire dire
autre chose que ce que montre l´objectif d´un appareil à photo.
La coîncidence de l´image photographique et de
l´image de synthèse 3D résulte de l´unicité du modèle qui les
fonde: L´optique géométrique dont les rayons ne sont pas moins
abstraits que ceux du ray tracing. L´identité des deux images
traduit simplement le parti pris "photo réalistique" de la synthèse.
En ne proposant que ce seul modèle aux artistes, les logiciels
de synthèse du commerce font l´impasse sur
toutes les découvertes de l´art moderne et les réflexions
d´un Panofsky ou d´un Francastel. On en revient ainsi à la notion
de mimesis, faisant du réalisme une nécessité de la représentation.
Mais cette vision réductrice n´est pas inscrite dans le
numérique et les récentes avancées en matière de programmation
(réseaux neuronaux, algorithmes et programmation génétiques),
de robotique et de vie artificielle, posent des problèmes autrement
plus cruciaux: Une machine peut-elle être intelligente,
un robot peut-il être vivant ? Il ne s´agit plus de reproduire
une apparence mais bien de construire une réalité.
La géométrie projective
Les artistes (peintres, graveurs et architectes) du XVe
siècle s´intéressèrent à la representation de l´espace sur un plan
à partir d´un oeil fixe et furent tout naturellement conduits
à étudier la projection centrale et à définir le
point de fuite comme l´image du point à l´infini dans la
direction perpendiculaire au plan du tableau, ce fut la perspective.
Celle-ci fut utilisée par l´architecture et la scénographie, mais
il faut attendre le XVII siècle pour qu´elle donne lieu
à une étude mathématique.
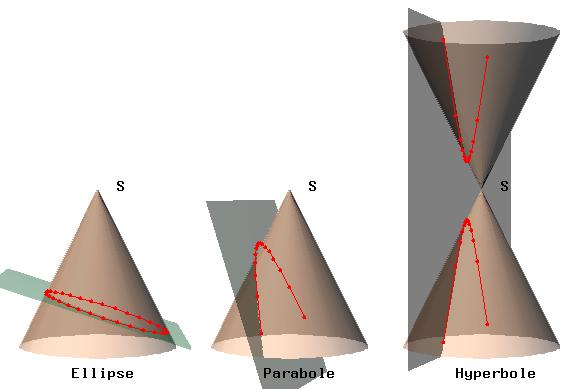
C´est le mathématicien français Desargues (1593-1662) qui est
considéré comme le véritable fondateur de la géométrie projective
avec son étude des coniques définies comme projections d´un cercle
(ou intersection d´un cône à base circulaire avec un plan)
reprise par Pascal en 1640:
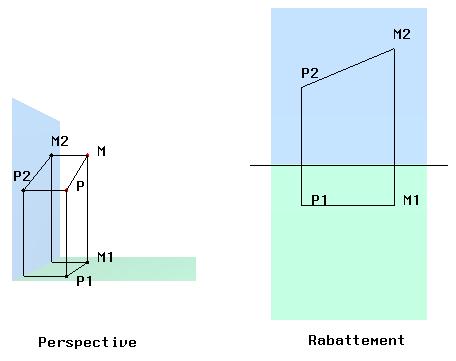
Beaucoup plus tard (fin du XVIIIe siècle), Monge invente la géométrie
descriptive qui représente l´espace par ses projections
cylindriques sur deux plans orthogonaux:
Poncelet (début du XIXe siècle) développe la géométrie projective
qui généralise les propriétés géométriques des figures de l´espace
aux éléments à l´infini ou imaginaires et qui étudie les invariants
géométriques par projection, c´est à dire les propriétés conservés par
projection: Ainsi l´alignement de 3 points est conservé,
mais le parallélisme ne l´est pas (Les projections de deux droites
parallèles sont deux droites concourantes):

Le mathématicien français Chasles (1793-1880) définit l´homographie
comme étant la transformation la plus générale transformant une droite
en une droite et un plan en un plan:
x´ = (a*x + b*y + c) / (d*x + e*y + f)
Les géométries non euclidiennes
Jusqu´au XVIIIe siècle le célèbre postulat des
parallèles d´Euclide (par un point extérieur à une droite on peut
mener une, et une seule, parallèle à cette droite) était considéré
comme démontrable.
Le mathématicien allemand Gauss (1777-1855) pense que la
géométrie est plus proche de la mécanique (basée sur l´observation)
que de l´arithmétique (basée sur la déduction) et met en doute
la démonstrabilité du postulat d´Euclide.
Le mathématicien russe Lobatchevski (1792-1856) montre en 1834
que le postulat des parallèles n´est pas impliqué par les fondements de
la géométrie et qu´il faut s´en remettre à l´expérience
(par exemple astronomique) pour le valider ou l´invalider. Il développe
la première géométrie non euclidienne.
Le mathématicien allemand Riemann (1826-1866) construit une
autre géométrie non euclidienne.
Le mathématicien allemand Klein (1849-1925) montre que les trois
géométries (celle d´Euclide, celle de Lobatchevski et celle de
Riemann) ne sont pas contradictoires. Elles correspondent respectivement
aux trois hypothèses de l´angle droit, de l´angle aïgu et de
l´angle obtu et peuvent s´interpréter par une courbure de l´espace,
elles sont équivalentes aux trois possibilités pour la somme des
angles d´un triangle: égale, inférieure ou supérieure
à 2*PI:

Enfin, avec le physicien américain Einstein (1879-1955) et sa théorie
de la Relativité, la géométrie de Riemann permet une représentation
de l´espace en accord avec les observations pratiques, ce que ne
pouvait pas faire la géométrie euclidienne.
Transformations géométriques
Les propriétés géométriques se caractérisent par les transformations
qui les laissent invariantes: Ainsi l´alignement pour la projection
centrale, les distances pour les déplacements, etc... Le
mathématicien français Evarist Galois (1811-1832) introduisit la
notion de groupe qui fut ensuite reprise par Klein en 1872 pour
hiérarchiser les transformations géométriques: Ainsi le groupe des
déplacements euclidiens (translations et rotations),
le groupe principal (translations, rotations
et symétries qui conservent les distances), le
groupe des similitudes (homothéties et translations), le groupe
affine (homographies qui conserve le parallélisme). Dans chaque
groupe la composition des transformations est une opération interne
associative, admettant un élément neutre (la transformation identique)
et chaque élément admet un inverse.
La perspective linéaire
Changements de repères
Soit RA = (A;xa,ya,za) le repère absolu (ou repère du monde).
Supposons un oeil ponctuel O donné par ses coordonnées
dans (RA) et regardant dans une direction (O,zo). Définissons le
repère de l´oeil (RO) par son centre O, l´axe (O,zo), l´axe (O,xo)
donné par son angle avec le plan horizontal (xa,ya), le troisième
axe (O,yo) s´obtient par le produit vectoriel des vecteurs unitaires
des deux précédents. Plaçons, perpendiculairement en un point E de l´axe zo et à
une distance D de O, un plan (P), appelé plan de projection.
Définissons le repère de l´écran (RE) par son centre E et ses
trois axes xe, ye et ze respectivement parallèles à xo, yo et zo.
Soit (S) une description géométrique d´une scène
(pour le moment
supposons qu´il s´agisse d´un ensemble de points 3D appelé geometrie
et d´un ensemble de relations appelé topologie). Appelons
perspective de (S) la projection centrale de (S) sur (P) de
pôle O. Si m est un point de (S), sa projection p est l´intersection
de la droite Om avec le plan (P). On voit, avec cette définition,
que les points du plan (xo,yo) passant par O et parallèle à (P) n´ont
pas de perspective:
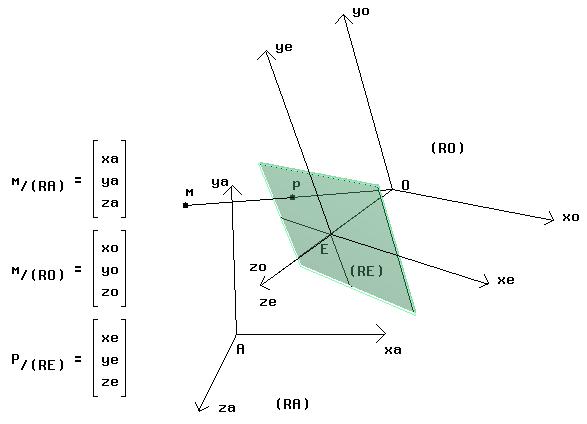
Soit PC la
matrice de passage
du repère (RA) au repère (RO), on a:
M/(RO) = PC * M/(RA)
Projection sur (P)
Soient (xo,yo,zo) les coordonnées d´un point m dans (RO) et soit
p sa projection sur (P). La figure suivante montre que les coordonnees
(xe,ye) de p dans le repère (E;xe,ye) verifient:
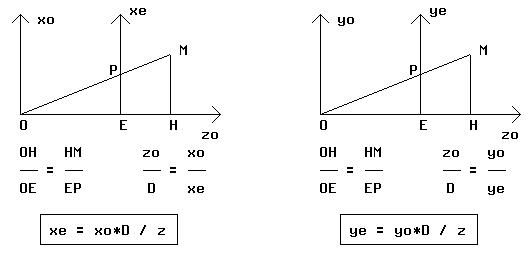
La projection, qui implique une division par z, n´est pas une
transformation linéaire et ne peut donc pas s´exprimer par une matrice.
Soit T le demi coté de la fenêtre de visualisation
supposée carrée,
on obtient des coordonnées normalisées (comprises entre -1.0 et 1.0)
en divisant par T:
xe = D*xo/(T*zo) et ye = D*yo/(T*zo)
Coupage
On appelle ouverture le rapport T/D = tan(an/2)
avec an = angle sous lequel l´oeil voit la fenêtre.
Soient [zmin,zmax] l´intervalle de variation des z. Le plan z=zmin
(avec zmin>0) est le plan de coupe proche, si zo > zmin alors la
division par zo est possible et ne donne pas lieu à un
débordement (division par un nombre trop petit), et, d´autre part, les points situés derrière l´oeil
(et qui donneraient une perspective inversée) sont ecartés. Le
plan z=zmax est le plan de coupe lointain, si zo < zmax alors la
division par zo ne donne pas lieu à un débordement
(division par un nombre trop grand). Les 4
plans passant par O et s´appuyant respectivement sur les 4 arêtes
de la fenêtre sont les plans de coupe latéraux d´équations:
x/z = T/D x/z = -T/D y/z = T/D et y/z = -T/D
Le volume
intérieur à la pyramide tronquée définie par ces 6 plans est appelée
pyramide de visualisation. Seule l´intersection de (S) avec ce
volume donne lieu à une projection perspective intérieure
à la fenêtre.
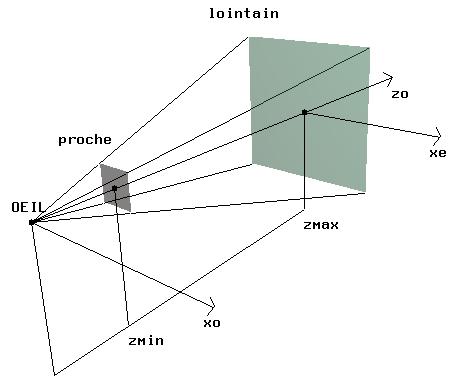
Perspective
La perspective a été définie comme la transformation homographique
transformant un plan en un plan. Le plan d´équation:
a*xo + b*yo + c*zo + d = 0
se transforme en le plan:
a´*xe + b´*ye + c´*ze + d´ = 0
où (xo,yo,zo) sont les coordonnées dans (RO) et (xe,ye,ze) sont les
coordonnées de la perspective.
On a vu plus haut (en La géométrie projective) que:
xe = D*xo/(T*zo) et ye=D*yo/(T*zo)
D´où
a´*D*xo/zo + b´*D*yo/zo + c´*zo + d´ = 0 soit encore:
ze = -d´/c´ - (a´*D*xo/zo + b´*D*yo/zo) / (c´*zo) qui est de la forme:
ze = p + q / zo
On choisit q<0 pour que zo et ze varient dans le même sens.
On normalise ze entre 0.0 et 1.0 lorsque zo varie de zmin à zmax:
zo=zmin implique ze=0: 0 = p + q/zmin soit q = zmin*zmax / (zmin-zmax)
zo=zmax implique ze=1: 1 = p + q/zmax soit p = -zmax / (zmin-zmax)
Cherchons (xe,ye) tels que:
xe = xo/w et ye = yo/w, d´ou
w = T*zo/D et par suite:
ze = p + q/zo = -zmax / (zmin-zmax) + zmin*zmax/(zo*(zmin-zmax))
ze = T*(zo/zmin-1)/((1-zmin/zmax)*w)
ou, sous forme matricielle (en
coordonnées homogènes):
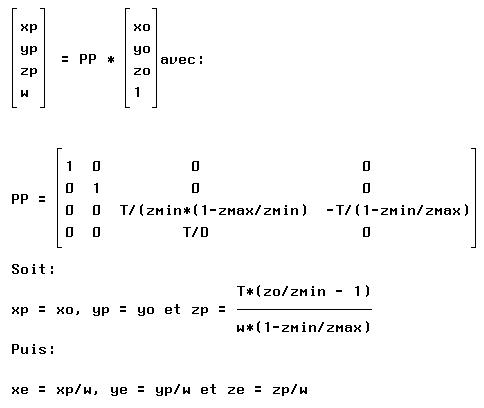
En résumé on passe du repère absolu (RA) au repère de l´oeil (RO)
par la matrice PC
puis de (RO) a un repère intermédiaire
(RP) par la matrice PP
On passe donc de (RA) a (RP) par la matrice
V = PP * PC
ce qui définit une transformation linéaire.
Puis on passe au repère de l´écran (PE) par une division par w,
qui n´est pas une opération linéaire.
Remarquons que les coordonnees(xp,yp) s´obtiennent par une projection
cylindrique d´axe zo de (xo,yo,zo).
Coupage (avant la division par w)
Alors que le coupage par la pyramide de visualisation.
nécessitait de calculer les intersctions de la scène (S) par 2 plans
verticaux (proche et lointain) et par 4 plans latéraux obliques, le
coupage réalisé sur les coordonnées (xp,yp) se fait en 2D par les
conditions:
-T <= xe <= T et -T <= ye <= T soit:
-T <= xp/w <=T et -T <= yp/w <= T soit:
-w*T <= xp <=w*T et -w*T <= yp <= w*T
Le coupage en z donne:
zmin <= ze <= zmax soit: zmin <= zp/w <= zmax, soit encore:
w*zmin <= zp <= w*zmax
Interprétation
La projection perspective peut être vue comme
une déformation de la scène (S) telle que sa projection
cylindrique sur le plan de projection (c´est à dire lorsque l´oeil
est à l´infini) coïncide avec sa projection perspective à partir de
l´oeil O.
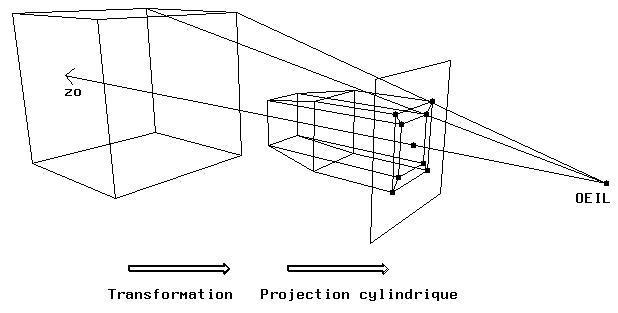
Les avantages de cette méthode sont:
1) Il n´y a qu´une seule matrice V réalisant le passage de (RA) a (RP)
2) Le coupage est plus simple (réduit en fait à des tests en 2D)
3) La projection se ramène finalement à une projection cylindrique
triviale.
4) On obtient la perspective par une simple division par w.















